 |
Fig.2.1 Cross section of a two-dimensional universe. |
Deriving an approximate expression for space curvature based on the "Big Spin" Model of Gravity and Newton's law of gravity
We will try to derive an approximate expression for space curvature. Our goal is to get a solution for "regular" gravity conditions, when Newtonian inverse square law applies. The following discussion will consider point masses for sake of simplicity.
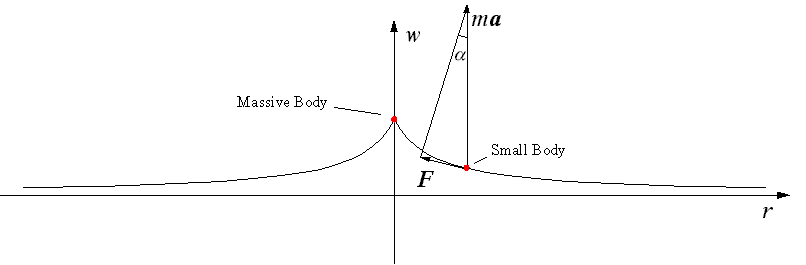
Again, for clarity and illustrating purposes we will refer to a picture of a two-dimensional “universe” analogy. Please take a look at Fig. 2.1. It presents a cross section of a fragment of a two-dimensional "universe". There is the Massive body, that curves space in its vicinity and the Small body, we neglect space curving for. To make our example more visually obvious, let's use centrifugal force instead of centripetal acceleration.
|
Fig.2.1 Cross section of a two-dimensional universe. |
Here F is a gravity force, ma is a centrifugal force, w is a displacement of the "universe" and r is a distance from the center of the Massive body. Let us also assume that displacement in direction w is small, thus distance between the bodies' centers as it is measured along the surface of the “universe” is approximately equal to the distance between projections of the bodies' centers on the axis r (this is an acceptable approximation for the relatively low gravity forces). Please keep in mind that our picture greatly exaggerates space bending in w direction.
F is a projection of ma on the "universe's hyperplane", so the value of F is
As 
is very small, we can apply that
From the definition of derivative and taking into account that angle between F and r
is equal to , it is easy to see that
for any point of the hypersurface of the "universe". Substituting, we have the following formula:
or substituting value of F with expression of Newton's law of gravity
integrating, we have the expression for space curvature:
With this formula, we still have some reservations for r = 0, similar to reservations for the Newton's law. Or perhaps I could suggest an exercise in curve-fitting, using the following formula:
where constants
and r0
could help to satisfy boundary conditions.
Very nicely, we can also see that displacement is proportional to mass M of the Massive body.
Although we referred to a 2D "universe" case, the formulas above will hold true for the 3D universe (bent in the direction of the fourth dimension) as well.
